After several months since I read S. Skinner’s book on sacred geometry, I have decided to compile my notes and reflections on everything the book revealed to me. Unlike previous occasions, I will not summarize the book or provide a fundamental opinion on topics widely covered in such works. Instead, I aim to share my personal thoughts and, where possible, add insights to what the book briefly indicates.
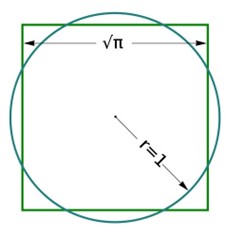
The main focus is understanding the reason behind divine proportions or, as I prefer to call them, “universal proportions.” My study of the golden ratio, pi, and e began during my primary education, like most of us, and expanded during high school. In 8th grade, we were first taught to draw a Nautilus, a prehistoric crustacean, using tools like a set square, ruler, and compass—a fitting initiation. Later, we learned that the relationship between a square’s diagonal and its rectangle leads to the golden ratio, a proportion used in art and construction since ancient times. Thanks to an extraordinary teacher, I discovered the problem of squaring the circle in high school with just a ruler and compass. Revisiting Skinner’s book, I’ve returned to this geometric problem, which, rather than distancing me from its solution, brings me closer to knowledge—it’s the journey that matters. This journey has led me to confront the elusive square root of pi. This geometric challenge serves as a link between ancient geometers and modern mathematicians, from the Pythagorean school to our times, passing through greats like Raphael. Why do I mention squaring the circle? Because I believe it symbolizes the connection between the divine and the human, primordial knowledge and our limited understanding. We continue pursuing it, knowing it is possible and that such knowledge exists. Arithmetically easy to verify, but geometrically still unresolved.
In the documentation I have read, aside from the book, on sacred geometry, there is constant reference to the Fibonacci sequence, the golden ratio, and nature’s order as signs of the divine surrounding us. This may be true, and indeed chaos theory shows us that starting from an initial point, we can obtain arbitrary sequences following the same pattern, as in fractals, but it can also lead to non-replicable exponential sequences—this is chaos. Therefore, we must not lose sight of our checkered floor, the black and white, as incorrect initial conditions will lead to degenerate, chaotic results. The importance of these natural patterns and proportions is that the G.·.A.·.D.·.U.·. has endowed humanity with the necessary perception to identify them, and I firmly believe that we all subconsciously recognize them. An example is the representations in cave paintings, most of which follow the natural proportions of the depicted images. This implies that the human mind is capable of reproducing what it perceives, and the alchemical fire within us allows us to represent proportions as we see them or as God conceived them. Another example that greatly impresses me is Vincent Van Gogh, who precisely depicted cascades of turbulence defined centuries later by Kolmogorov. Turbulence scales describe the energy loss in turbulence. A simple example is a plume of cigarette smoke, where large swirls at first gradually break into smaller ones due to fluid energy loss. This decomposition and the size of the vortices are exact, depending on the fluid and initial conditions. Yet, Van Gogh, without knowing this, accurately represented a perfect turbulence scale in paintings like The Starry Night. To me, this proves humanity’s ability to assimilate and analyze its surroundings, carrying within us the primordial or secret knowledge we have sought since the beginning of time. Therefore, we must look within ourselves to find the path to this knowledge.
Just as geometry is present in nature, the earthly realm, arithmetic resides in ideas, the divine realm. Every geometric representation must have a mathematical or arithmetic explanation. In this sense, the evolution of geometric knowledge has also advanced arithmetic and other sciences like physics. From my perspective, the author of the book in our bibliography does not delve into this topic deeply enough. Mathematical concepts like nothingness, unity, duality, or numerology are also part of sacred geometry or the temples preserved today. A clear example is the use of the number 8, symbolizing infinity, in oriental constructions that reached the West through orders like the Templars or directly through Arab architecture in the Iberian Peninsula. We must not forget that Arab architecture was heavily influenced by geometric knowledge derived from ancient Greek studies. It was through this knowledge that the study of Greek culture reemerged in Europe via Al-Andalus.
The beginning of the book was particularly interesting to me for its depiction of how mathematical studies were approached in ancient times and how knowledge was transmitted by Pythagorean schools. Topics such as fundamental arithmetic or measurement methods from a pre-decimal system era are areas I would like to explore in future readings.
Without delving into the section on cathedral geometry, the part of sacred geometry that most captured my attention concerns the dimensions of King Solomon’s Temple.